【51CTO.com快译】Swift算法俱乐部(https://github.com/raywenderlich/swift-algorithm-club)是一个开放源码项目,其目的是使用Swift语言实现一些常用的算法和数据结构。
在每个月份,SAC团队都会在www.raywenderlich.com网站上以教程形式公布一个很酷的数据结构或算法。因此,如果您想要了解更多关于Swift语言实现的算法和数据结构,您可以一直关注这个网站。
在本教程中,你将学习一种经典的搜索和寻路算法,即广度优先搜索算法。
广度优先搜索算法最初是由克里斯·皮尔策(Chris Pilcher,https://github.com/chris-pilcher)实现的。在本教程中,我们将根据需要对其实现格式方面稍加重构。
本教程假定您已经了解基于Swift语言实现的图论中的邻接表算法(https://www.raywenderlich.com/152046/swift-algorithm-club-graphs-adjacency-list)和队列算法(https://www.raywenderlich.com/148141/swift-algorithm-club-swift-queue-data-structure),或具有相类似的基础知识。
注意,如果您对Swift算法俱乐部感兴趣并且是新手,您可以访问这个地址https://www.raywenderlich.com/135533/join-swift-algorithm-club。
入门
在Swift图论邻接表算法(https://www.raywenderlich.com/152046/swift-algorithm-club-graphs-adjacency-list)中,我们提出了一种描述图中的各对象及其间关系的方法。在一个图中,每个对象表示为一个顶点,而每个关系表示为一条边。
例如,可以用图来描述一个迷宫。在迷宫中的每个接合点可以由一个顶点来描述,而接合点之间的每个通道可以使用边来描述。

广度优先搜索是在1950年被E. F. Moore(https://en.wikipedia.org/wiki/Edward_F._Moore)发现的,这种算法并不只是为了寻找一条穿过迷宫的通路,而是为了寻找穿越迷宫的最短路径的算法。此广度优先搜索算法背后的想法倒是很简单的︰
搜索围绕从某一源点出发的一组移动对应的每一个位置。
然后,以增量步长方式修改这个数字,直到找到目的地。
下面,让我们来分析一下具体的例子。
举例
假设你是在一个迷宫的入口处,请参考下图。
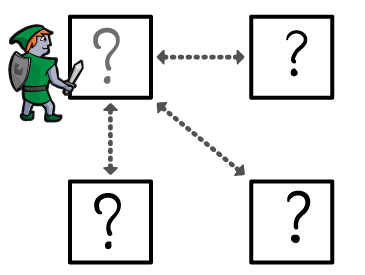
广度优先搜索算法以如下方式工作︰
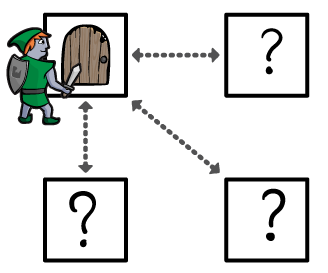
1. 搜索你的当前位置。如果这是目的地,则停止搜索。
2.搜索您所在位置的邻点位置。如果其中任何之一是目的地,则停止搜索。

3.搜索这些位置的所有邻接点位置。如果任何其中之一是目的地,则停止搜索。
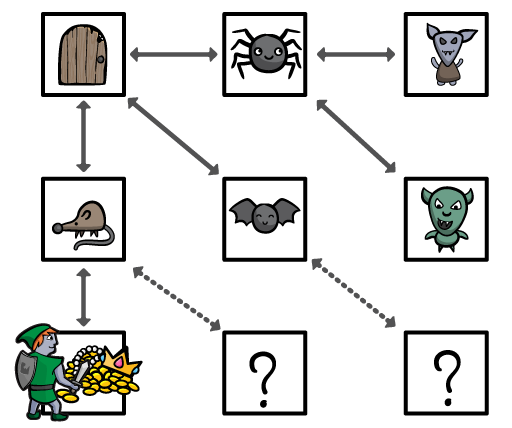
4.最后,如果存在一条到达目的地的路线,则称发现了一条通路,并以从原点出发的最少移动步数存储起这条通道。如果你已经用完了要搜索的位置,则说明不存在一条到达目标的的通路。
【注】就广度优先搜索算法而言,最短路线是指从一个位置到达下一个位置的最少移动步数。
在我们提供的迷宫例子中,广度优先搜索算法认为迷宫中房间之间的所有通道都具有相同的长度,当然是实际中这可能不是真实的。你可以把通过迷宫的最短路线看作最短方向列表,而不是最短的距离。
在未来的教程中,我们将探索最短距离的路径寻找算法。
Swift广度优先搜索算法
从现在开始,让我们具体分析一下基于Swift语言实现的广度优先搜索算法。
为此,请先下载本教程的初始源码(https://koenig-media.raywenderlich.com/uploads/2017/03/BreadthFirstSearch-Start.playground.zip),其中提供了基于Swift语言实现的邻接表和队列的数据结构。
【注意】如果你想了解Swift语言实现的邻接表和队列的数据结构是如何工作的,你可以使用命令View\Navigators\ Show Project Navigator来分析有关代码。您还可以具体学习如何使用Swift语言构建这些邻接表和队列教程。
首先,我们定义一个名为Graphable的协议;所有的图形数据结构都要遵从该协议。然后,我们要扩展该协议;这样一来,我们可以将广度优先搜索应用于所有的图类型中。
下面是Graphable协议看起来的样子︰
public protocol Graphable {
associatedtype Element: Hashable
var description: CustomStringConvertible { get }
func createVertex(data: Element) -> Vertex<Element>
func add(_ type: EdgeType, from source: Vertex<Element>, to destination: Vertex<Element>, weight: Double?)
func weight(from source: Vertex<Element>, to destination: Vertex<Element>) -> Double?
func edges(from source: Vertex<Element>) -> [Edge<Element>]?
}在上面下载的初始示例工程的较靠上的位置(在语句 import XCPlayground的后面即可),创建我们的扩展:
extension Graphable {
public func breadthFirstSearch(from source: Vertex<Element>, to destination: Vertex<Element>)
-> [Edge<Element>]? {
}
}让我们概括一下此函数签名︰
其中声明了一个函数,它接收两个顶点参数:第一个是源点,即我们的出发点;第二个是目标点,即我们的目标。此函数返回一条以边对象形式组成的路线(从源点出发直到目标位置)。
如果路线存在,我们还指望它以排序方式存储!路线中的第一条边将从源顶点开始,而路线中的最后一条边将以目标顶点终结。对于路线中的每一对相邻边,第一条边的目的点将与第二条边的源点成为同一顶点。
如果源点与目的点是一样的,则说明这条路线是一个空数组。
如果路线不存在,该函数应返回nil。
广度优先搜索依赖于按正确的顺序访问的顶点。要访问的第一个顶点总是对应于源点。之后,我们会分析源点的邻结点;然后,以此类推下去。我们每访问一个顶点,便将其结点添加到队列的后面。
因为我们此前已经了解了队列知识,所以这里我们可以直接使用它!
于是,我们可以把上面的函数更新成下面这样︰
public func breadthFirstSearch(from source: Vertex<Element>, to destination: Vertex<Element>)
-> [Edge<Element>]? {
var queue = Queue<Vertex<Element>>()
queue.enqueue(source) // 1
while let visitedVertex = queue.dequeue() { // 2
if visitedVertex == destination { // 3
return []
}
// TODO...
}
return nil // 4
}下面,我们来逐步分析一下上面的代码:
1. 首先,创建一个顶点队列,并把源点加入队列。
2. 从队列中出列一个顶点(只要队列非空),并称之为访问顶点。
3. 在首次迭代中,访问顶点将是源点,而且队列会立即为空。然而,如果访问源结点添加更多的结点,则搜索会继续进行下去。
4. 检测是否访问顶点是目标顶点。如果是,则立即结束搜索。目前情况下,你将返回一个空的列表——这与目标结点找到时是一样的情况。然后,将构造一条更为细致的线路。
5. 如果队列中顶点为空,则返回nil。这意味着,目标结点没有找到;有可能不存在相对于它的一条通路。
接下来,我们需要把访问结点的所有邻居结点加入队列中。为此,可以使用如下代码:
let neighbourEdges = edges(from: visitedVertex) ?? [] // 1
for edge in neighbourEdges {
queue.enqueue(edge.destination)
} // 2再让我们作细致的分析:
1.这里使用Graphable协议的edges(from:)函数来取得访问结点的边数组。记住,edges(from:)函数返回的是一个可选的边数组。这意味着,如果此该数组为空,或者nil,则不存在以此结点开始的边。
因为(为了我们的搜索目的)空表和nil意思一样——没有邻结点可入队列;所以,我们使用一个空列表来nil聚合可选数组,从而去掉可选功能。
2.现在,你可以在边列表上安全地进行for循环迭代,从而把每一个边的目标结点入队列。
到此,我们的任务还没有完全完成。事实上,在此搜索算法中还存在一处微妙的危险!如果你在此示例中运行搜索算法会遇到什么问题呢?在此,我们可以不考虑这样一个事实,即宝物房间没有关连到图上。
我们不妨去手工方式推算一下每当我们访问一个顶点时将会发生什么。

如果你在此示例中运行搜索算法会遇到什么问题呢?答案如下:
1. 宽度优先搜索算法将创建一个队列,并把入口处房间入队列。
2. 当第一次进入到while循环时,我们把入口房间出队列并访问它。入口房间中不存在宝物,这样我们可以搜索入口房间的所有邻居房间。入口房间有一个邻居房间,即蜘蛛房间。于是,我们把它入队列。
3. 当第二次进入到while循环时,我们把蜘蛛房间出队列并访问它。因为蜘蛛房间中也没有宝物,所以我们进一步搜索蜘蛛房间的所有邻居房间。蜘蛛房间有一个邻居房间,即入口房间,于是我们把它入队列。
4. 当第三次进入到while循环时,我们把入口房间出队列……
问题是:我们以前已经达到过这个位置了!
为了修正这个问题,我们需要记下我们曾经访问过的顶点信息,以便我们确保不会第二次访问它们。
有好几种办法可以解决这个问题。你可以像如下这样更新你的代码:
public func breadthFirstSearch(from source: Vertex<Element>, to destination: Vertex<Element>) -> [Edge<Element>]? {
var queue = Queue<Vertex<Element>>()
queue.enqueue(source)
var enqueuedVertices = Set<Vertex<Element>>() // 1
while let visitedVertex = queue.dequeue() {
if visitedVertex == destination {
return []
}
let neighbourEdges = edges(from: visitedVertex) ?? []
for edge in neighbourEdges {
if !enqueuedVertices.contains(edge.destination) { // 2
enqueuedVertices.insert(visitedVertex) // 3
queue.enqueue(edge.destination)
}
}
}
return nil
}让我们回顾一下发生了什么变化︰
1.上面的代码将创建一个顶点数组,用来描述到目前为止你遇到过的顶点的列表。请记住,Vertex类型是Hashable,所以我们不需要做任何更多的工作来构建一个顶点集。
2.每当检查相邻的顶点,都要首先检查此前是否遇到过该结点。
3.如果你以前没有遇到过该结点,则将它添加到两个队列中:要处理的顶点列表(队列结构)和遇到的顶点列表(enqueuedVertices)。
这意味着,上面的搜索算法是相当安全的。但是,现在你还不能访问比开始的那个图中更多的顶点,因此搜索最终必须终止。
发现回路
我们的算法快要成功了!
到目前为止,你已经知道如果找不到目的地,你会返回一个nil值。但是,如果你找到了目的地,你需要找到你的往回走的线路。不幸的是,每个你访问过的房间都已经出队列了,对于如何找到目的地没有留下任何记录信息!
为了记录下搜索信息,你需要使用一个字典结构来替换你搜索过的顶点集合,其中需要包含所有您搜索过的顶点信息和你如何到达该顶点的信息。我们不妨把这想像为探索一个迷宫,使用一个带箭头的粉笔标记指向所有你探索过的房间——通过这种方式来记忆下到达入口处的所有信息。
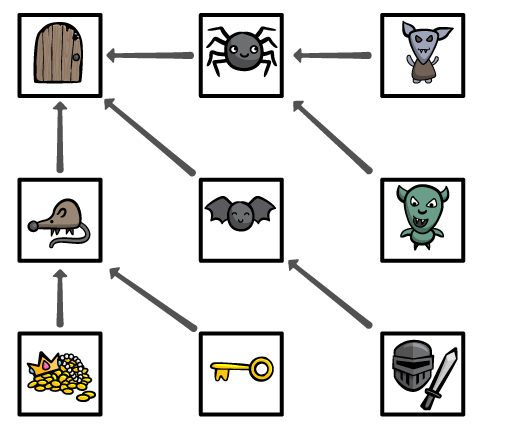
如果我们保持跟踪所有的箭头——针对我们访问过的任何房间,我们只可以查找我们沿着到达它的边缘。这个边将引回到我们早些时候访问过的房间。当然,我们也可以查找我们沿着到达它的边,如此下去……直到开头的那一条边。
让我们来试试这种想法——创建下面的Visit枚举类型。注意,你必须在Graphable扩展的外部创建这个类型,因为Swift 3不支持嵌套泛型类型。
enum Visit<Element: Hashable> {
case source
case edge(Edge<Element>)
}在我们的查询表中,第一列中的每个项都是一个顶点(Vertex),但第二列中的每个项并不都是一条边(Edge);一个顶点(Vertex)总是源顶点;否则,就会出现严重的错误,从而导致我们永远走不出图去!
接下来,按照如下所示修改您的方法︰
public func breadthFirstSearch(from source: Vertex<Element>, to destination: Vertex<Element>) -> [Edge<Element>]? {
var queue = Queue<Vertex<Element>>()
queue.enqueue(source)
var visits : [Vertex<Element> : Visit<Element>] = [source: .source] // 1
while let visitedVertex = queue.dequeue() {
// TODO: Replace this...
if visitedVertex == destination {
return []
}
let neighbourEdges = edges(from: visitedVertex) ?? []
for edge in neighbourEdges {
if visits[edge.destination] == nil { // 2
queue.enqueue(edge.destination)
visits[edge.destination] = .edge(edge) // 3
}
}
}
return nil
}让我们回顾一下上面的代码中发生了什么变化︰
1. 这将创建一个对应于Vertex键和Visit值的字典,并使用源顶点作为从“源点”处的访问来初始化这个字典。
2. 如果字典里没有对应于某一个顶点的入口,那么说明此顶点还没有加入队列。
3. 每当你入队一个顶点时,你并不只是把它放进一个顶点集合中,还要记录下到达它对应的边。
最后,你可以从目标到入口进行回溯!并且使用TODO注释处的实际代码来更新if语句︰
if visitedVertex == destination {
var vertex = destination // 1
var route : [Edge<Element>] = [] // 2
while let visit = visits[vertex],
case .edge(let edge) = visit { // 3
route = [edge] + route
vertex = edge.source // 4
}
return route // 5
}让我们分析一下上面的代码︰
1.首先创建一个新的变量,用来存储作为路线的一部分的每个顶点。
2.还要创建一个变量来存储路线。
3.创建一个while循环;只要访问字典有一个顶点入口并且只要此入口是一条边,则该循环将会继续下去。如果该入口是一个源点,则该while循环将结束。
4.把边添加到你的路线的开头,并把顶点设置为该边的源点。现在,你距离开始处更接近了一步。
5.while循环结束;所以,你的路线现在也必须完成。

到此为止,我们解决了所有问题!你可以在示例工程文件的结束处加入如下代码来进行测试:
if let edges = dungeon.breadthFirstSearch(from: entranceRoom, to: treasureRoom) {
for edge in edges {
print("\(edge.source) -> \(edge.destination)")
}
}相应地,你应当在控制台上观察到如下的输出结果:
Entrance -> Rat Rat -> Treasure
小结
我真心希望广大读者朋友能够喜欢本教程提供的基于Swift语言的广度优先搜索算法!
在本教程中,我们已经扩展了所有Graphable数据类型的行为,所以您可以搜索从任一顶点到任何其他顶点的路线。更妙的是,你得到的是一条拥有最少步数的路线。
你可以从网址https://koenig-media.raywenderlich.com/uploads/2017/03/BreadthFirstSearch-Final.playground.zip处下载包含所有上述代码的改进的示例工程源码。你也可以在Swift算法俱乐部存储库中找到原始广度优先搜索算法的原始实现代码并参与进一步讨论。
事实上,这个算法仅仅是Swift算法俱乐部存储库中的一个小部分,感兴趣的读者可以进一步查阅这些代码库(https://github.com/raywenderlich/swift-algorithm-club)。
【51CTO译稿,合作站点转载请注明原文译者和出处为51CTO.com】
http://mobile.51cto.com/iphone-535133.htm
最新评论: